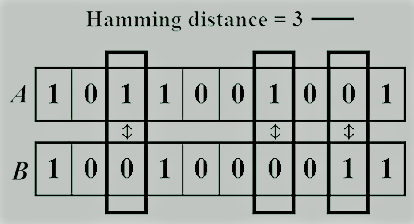
Hamming Distance
Hamming Distance is a metric to compare two binary data strings. Comparing two equal-length binary strings. It has the number of bit locations in which all bits differ.
The gap Hamming between two strings, a and b have indicated as d (a,b).
This has used as the data have passed over computing networks for error detection or error correction. In coding theory, it has often used to compares data terms of equivalent length.
Calculation of Hamming Distance
We execute their XOR function (a line b) and count then the total number of 1s in the resulting string to determine a hamming distance of two strands.
Example
Suppose there are two strings 1101 1001 and 1001 1101.
11011001 ⊕ 10011101 = 01000100. Since, this contains two 1s, the Hamming distance, d(11011001, 10011101) = 2.
Minimum Hamming Distance
The minimum hamming distance is the smallest in a series of strings of equivalent lengths of all possible string pairs.
Example
Suppose there are four strings 010, 011, 101 and 111.
011 ⊕ 101 = 110, d(011, 101) = 2.
011 ⊕ 111 = 100, d(011, 111) = 1.
101 ⊕ 111 = 010, d(011, 111) = 1.
Hence, the Minimum Hamming Distance, dmin = 1.
The system state from Hamming has used to describe such basic notions, such as error detection and error correction, in the coding theory. Code C has said to be a k mistake, especially if at least the minimum distance of hamming is k+1 between two of its code names.
Take the code of two codes “000” and “111,” for instance. The difference between the two terms has 3 so that the error has found in k=2. This means that the error have observed where one bit has reversed or two bits have been reversed. Just “000” has “111” and the mistake cannot detected until the three bits have changed.
A code C has said to be k-errors if there has at most one codeword c for every word w in Hamming space, such that is at maximum k. In other words, k-errors are used to correct code only where the minimum distance from Hamming is at least 2 k+1 for two of its codewords. This has geometrically more readily understood as any closed radius k ball that focuses on distinct codewords has disjointed. In this case, these balls have also known as hamming spheres.
For example, take a 3-bit code with two “000” and “111” coding terms into consideration. Hamming has made up of eight thousand, 001, 010, 011, 100, 101, 110, and 111 words. The coding word “000” and the single-bit error words “001”,”010″, “100” both have a distance between 1 and “000” The codeword “111” has also used in 1 Hamming distance from the original “111” with its single bit mistaken words “110,” 101″ and “011.” A single bit of error within 1 hamming distance from the original codes is always in this code and the code will correct one error, i.e. k=1. The minimum gap from “000” to “111” from “000” is 3, satisfying 2k+1 = 3.
This way a code with the minimal gap d of Hamming between its code names will often detect d-1 bugs and right ̈false ̈(d-1)/2 ̈. The latter number has also known as the packaging radius or the code correction feature.