Notation
Notation: In analyzing the time and space complexity of an algorithm. We will never offer accurate numbers to set the time and space that the algorithm requires. Instead of utilizing certain common notations, also known as Asymptotic Notations.
When we analyze an algorithm, we often receive a format that shows the time needed to execute the algorithm. The number of memory accesses, the number of comparisons, the time necessary for the computer to execute the algorithm code. Often this formula comprises insignificant information that does not actually tell us the time it takes.
Take an example, if some algorithms have a T(n) = (n2 + 3n + 4) time complexity, which is a quadratic equation. The 3n + 4 part is negligible compared to the n2 part for the big values of n.
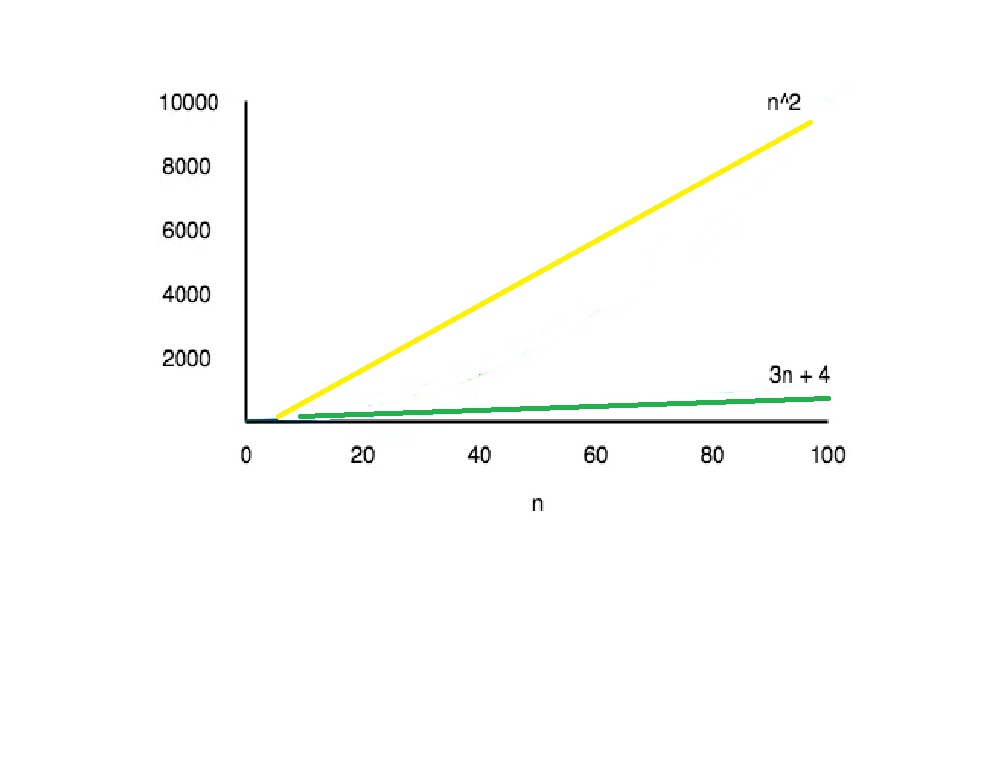
For n = 1000, n2 will have 1000000 while 3n + 4 will have 3004.
In addition, the consistent coefficients of higher-order terms are similarly disregarded. When compared with the execution durations of the two methods.
A 200 n2 the method takes a time quicker than some other n3 time algorithm, for a value greater than 200 n. Since we are concerned solely with the asymptotic behavior of the function growth, we also may disregard the constant factor.
Asymptotic Behaviour
The phrase asymptotic implies to randomly approach a value or curve (i.e., as some sort of limit is taken).
Remember that in high school you study limits, it is the same thing.
The only difference here is that we do not have to find the value of any expression. Where n is near a limit or infinity. But we use the same model in the event of asymptotic notations, to ignore the constant factors. The insignificant portions of an expression and development in a single coefficient. A better way of representing the complexities of algorithms.
To explain this, let’s take an example:
If we have two algorithms that show the time necessary for the execution of the following expressions:
Expression 1: (20n2 + 3n – 4)
Expression 2: (n3 + 100n – 2)
Now we need only worry about how the function will expand. When the value of n(input) increases, and that depends solely on Expression 1 n2 and Expression 2 n3. Therefore we can claim that merely analyzing the most power-coefficient and disregarding. Other constants(20 in 20n2), and inconsequential portions, for which time-run is represented by the formula 2. Will be quicker than the other approach (3n – 4 and 100n – 2).
The key concept to get things manageable is to toss aside the less important component. All we need to do is analyze the method first to get the expression. Then analyze how it grows with the growth of the input(s).
Types of Notations
In order to reflect the growth of any algorithm. We use three kinds of asymptotic. Notations as to the input increase:
- The Big Theta Notation (Θ)
- The Big Oh Notation (O)
- Big Omega Notation (Ω)
Big Theta Notation (Θ)
When we state that the timescales indicated by the large notation are tight. We imply that the time competitiveness is like the mean value or range within. Which time the algorithm will really executed.
For example, if the complexity of the time has expressed in an algorithm by equation 3n2 + 5n and we are using this Big- Tel notation, then the complexity of the time would be the same (n2), disregarding the constant-coefficient and omitting the unimportant component, which is 5n.
This indicates that the time for access to any input n is between k1 * n2 and k2 * n2, where k1, k2 have two constants, and that this means that the equation representing the development of the algorithm has tightly bound.
Big Oh Notation (O)
The top limit of the algorithm or worst case of a method has known as this notation.
It informs us that for every number of n, a given function is never longer than a certain duration.
Therefore, since we already have the large notation, which is a very nightmare for all algorithms, we require this representation. The question is: To explain that, let’s take a simple example.
Consider the Linear Search method for an array item, searching for a specified number one by one.
In the worst scenario, we discover the element or number. We are looking for at the end, beginning on the foreside of the table. This leads to a time complexity of n, where n indicates the number of total items.
However, the element that we look for is the first member in the array, thus the time complexity is 1.
In this case, now, saying that the large-to-band or close-bound time complexity for linear search is a total iv(n). Will always mean that the time needed is related to n. Since that is the correct way to represent the average time complexity. But if we use the great-to-band notation, we mean that the time complexity is O (n).
This is why most of the time because it makes more sense. The Big-O notation has used to describe the time complexity of any method.
Big Omega Notation (Ω)
Big Omega notation has used to define any algorithm’s lower limit. We can tell the best case using any algorithm.
This shows the least necessary time for each method, hence the best case of any algorithm, for all input values.
In simple words, if we are a time complexity in the form of a large-talk for any algorithm. We mean the algorithm takes at least that much time to perform. It can certainly take longer than that.